Equations de Navier-stokes
- Amenosphis Doué
- 19 févr. 2016
- 3 min de lecture

LA MYSTERIEUSE EQUATION DE NAVIER-STOKES :
En mécanique des fluides, les équations de Navier-Stokes sont des équations aux dérivées partielles non linéaires qui sont censées décrire le mouvement des fluides « newtoniens » (liquide et gaz visqueux ordinaires) dans l’approximation des milieux continus. La résolution de ces équations modélisant un fluide comme un milieu continu à une seule phase incompressible, si elle est possible, est ardue. La cohérence mathématique de ces équations non linéaires n'est pas démontrée. Mais elles permettent souvent par une résolution approchée de proposer une modélisation des courants océaniques et des mouvements des masses d'air de l'atmosphère pour les météorologistes, la simulation numérique du comportement des gratte-ciel ou des ponts sous l'action du vent pour les architectes et ingénieurs, des avions, trains ou voitures à grandes vitesse pour leurs bureaux d'études concepteurs, mais aussi le trivial écoulement de l'eau dans un tuyau et de nombreux autres phénomènes d'écoulement de divers fluides. Elles sont nommées d'après deux scientifiques du xixe siècle, le mathématicien et ingénieur des Ponts, Claude Navier et le physicien George Stokes, le choix oubliant le rôle intermédiaire du physicien Adhémar Barré de Saint-Venant. Pour un gaz peu dense, il est possible de dériver ces équations à partir de l’équation de Boltzmann, décrivant un comportement moyen des particules dans le cadre de sa théorie cinétique des gaz. La résolution des équations de Navier-Stokes constitue l'un des problèmes du prix du millénaire.
Pourquoi l’équation est-elle si compliquée ?
Il y a deux manières de comprendre pourquoi l’équation de Navier-Stokes est compliquée : la vision mathématique et la vision physique. Pour le mathématicien, l’équation est compliquée parce que c’est une équation différentielle non-linéaire. Si vous la comparez à l’équation qui décrit le mouvement d’un ressort (ou même, pour ceux qui connaissent, à l’équation de Maxwell ou à celle de la chaleur), la complication vient du terme . Ce terme varie comme le carré du champ de vitesse, et c’est lui qui rend l’équation mathématiquement inextricable. En maths, la non-linéarité complique les choses, mais en physique aussi ! Car ce terme non-linéaire a sa traduction dans la complexité des phénomènes physiques. l’équation de Navier-Stokes sert surtout à décrire le mouvement des fluides.
A quoi ressemble l’équation ?
Pour les non-initiés, la forme de l’équation est un peu rebutante, mais l’important est de comprendre en gros ce qu’elle représente. En mécanique, quand on étudie le mouvement des skieurs, des ressorts ou des boulets de canons, on écrit la loi de Newton « Somme des forces = ma » où m est la masse et a l’accélération.L’équation de Navier-Stokes ne dit pas autre chose que « Somme des forces = ma », mais comme on parle du champ de vitesse d’un fluide, la forme est un peu plus compliquée que pour un boulet de canon.
Dans un fluide, on va considérer deux types de forces : les forces de pression et les forces visqueuses. Les forces de pression, ce sont celles qui viennent du fait qu’un petit morceau du fluide se fait pousser par tout le reste du fluide qui l’entoure. Les forces visqueuses, ce sont l’équivalent des forces de frottement pour un skieur. Quand un morceau de fluide glisse sur un autre, il y a un frottement qui le freine et qui est d’autant plus important que le fluide est visqueux. Dans l’équation, on verra donc apparaître un paramètre qui représente la viscosité du fluide.
Voici donc l’équation de Navier-Stokes, et en quoi elle est l’analogue de « Somme des forces = m a » pour un fluide :
Ici est le champ de vitesse, est la pression, la masse volumique du fluide et sa viscosité. Encore une fois, vous n’êtes pas obligés de piger les détails de l’équation, mais nous allons considérer globalement ses propriétés, et voir ce qu’on peut en dire.
[Petite remarque pour ceux qui connaissent les EDP : la pression est aussi une inconnue de l’équation. Comme le champ de vitesse a 3 composantes, cela fait 4 inconnues pour 3 équations. Il manque donc une équation ! Si on suppose le fluide incompressible, il faut ajouter une condition qui est que le champ de vitesse est de divergence nulle – ce qui traduit aussi la conservation de la masse]















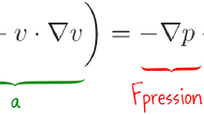

Commentaires